【ラビットチャレンジ】 深層学習：その4 Day4まとめ

ラビットチャレンジ 深層学習：その4

講師の人

レコメンドエンジンを開発

TensorFlowについても少しふれていく

TensorFlowの使い方

実際の業務ではニューラルネットワークを実装するラッパー、ミドルウェアを利用することがほとんど

TensorFlowはユーザー数が一番多い

※ tensorflowインストール

pip3 install --upgrade tensorflow --ignore-installed
python
 >> import tensorflow as tf
 (何事もなく完了)

※ 以下tensorflowの基本的な概念や使い方を列挙

constant

a = tf.constant(1)
b = tf.constant(2, dtype=tf.float32, shape=[3,2])
c = tf.constant(np.arange(4), dtype=tf.float32, shape=[2,2])

constantの第一引数、初期化するパラメータ 第二引数、パラメータのタイプ 第三引数、テンソルのかたち

デバッグについて → 基本的にはprintデバッグ

placeholder

箱のようなもの。

# プレースホルダーを定義
x = tf.placeholder(dtype=tf.float32, shape=[None,3])

variables

変数

# 変数を定義
x = tf.Variable(1)

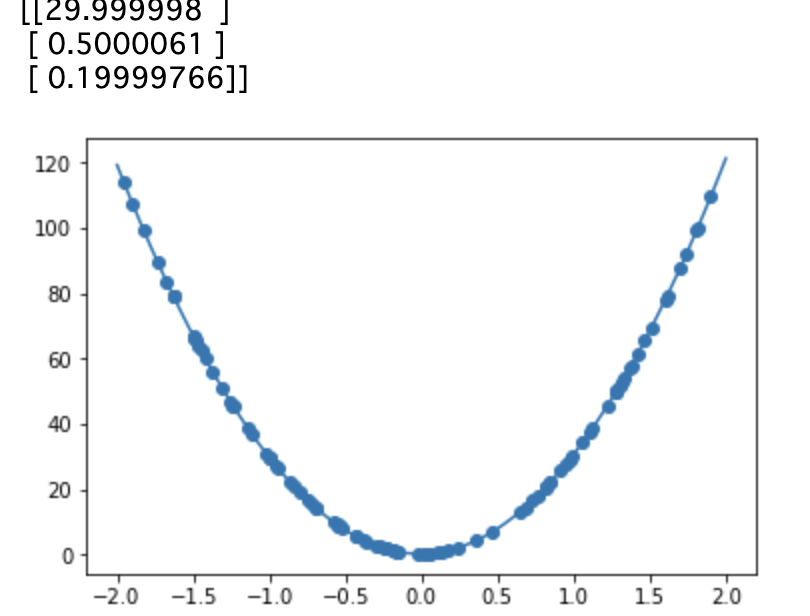
線形回帰

noise=0.3

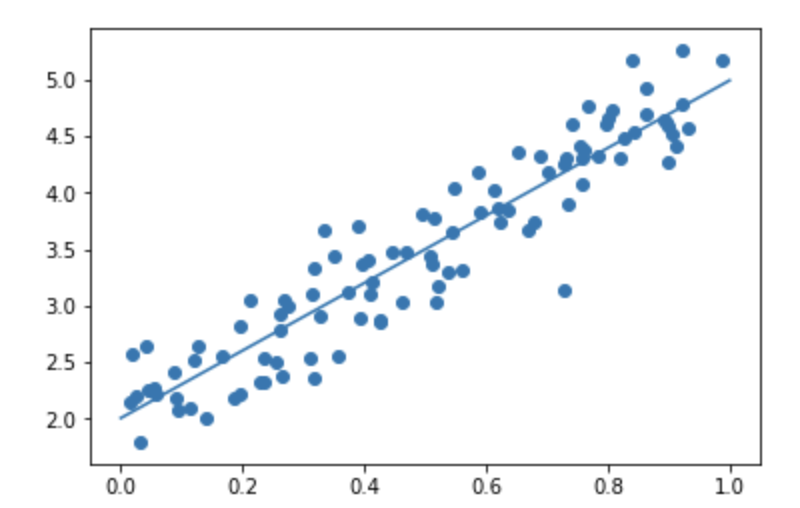
noise=0.1

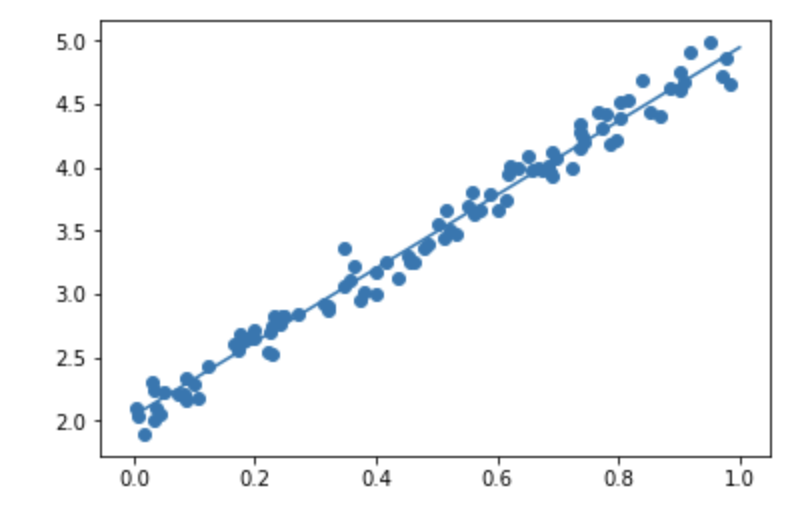
d=5x+2, noise=0.1

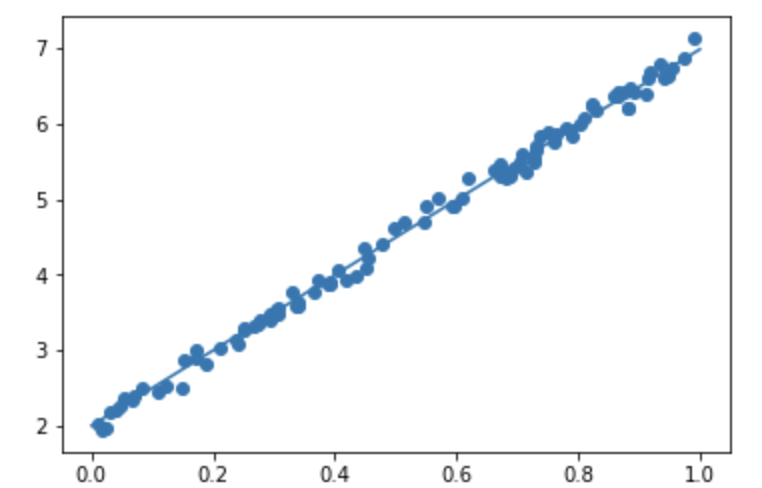
非線形回帰

noise = 0.05

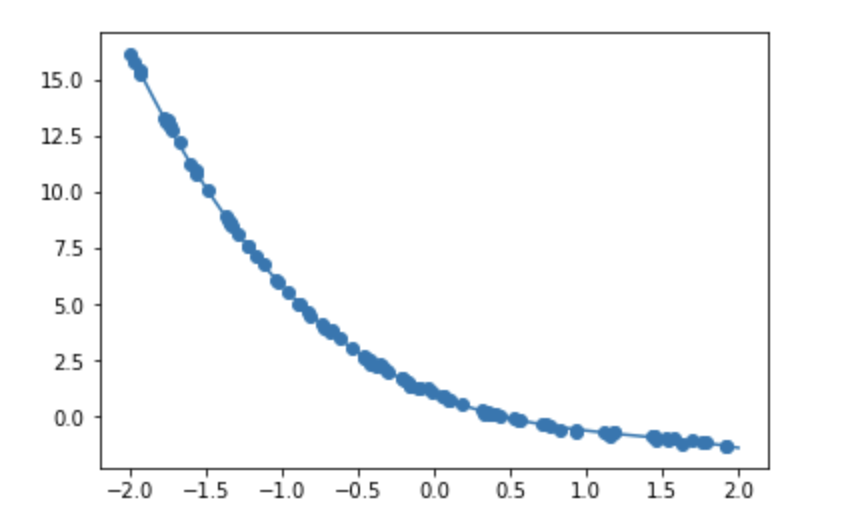
noise = 0.6

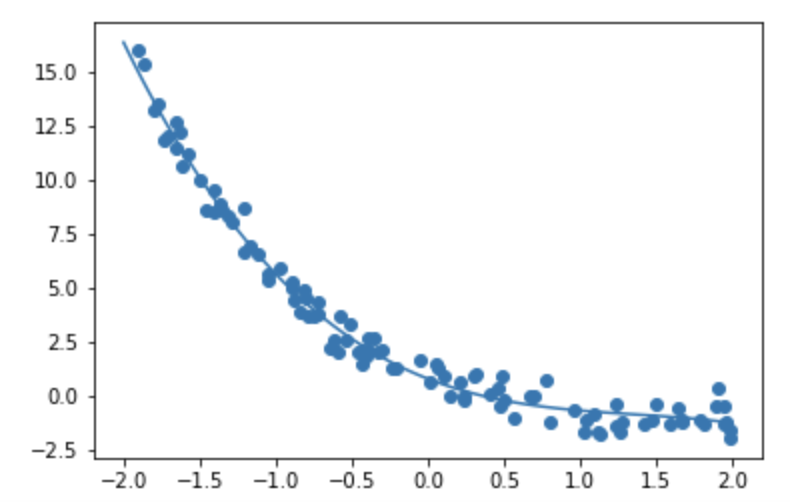
演習問題

TensorFlowによるMNIST

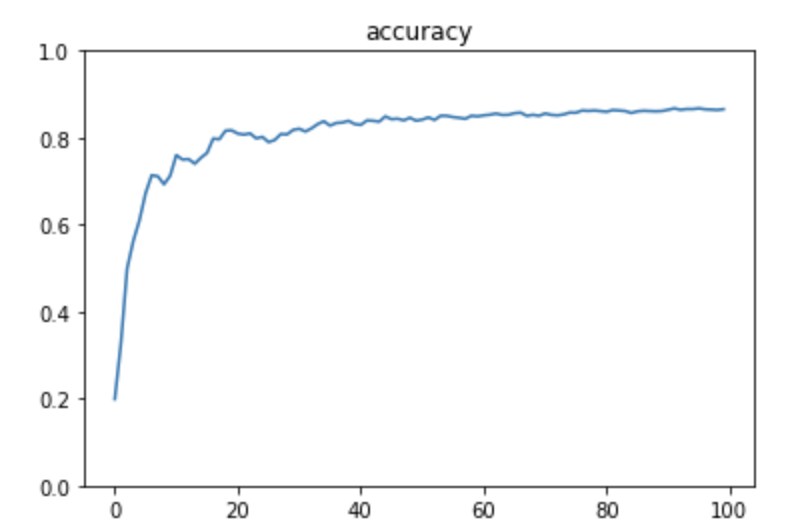
1層

3層(Adam)

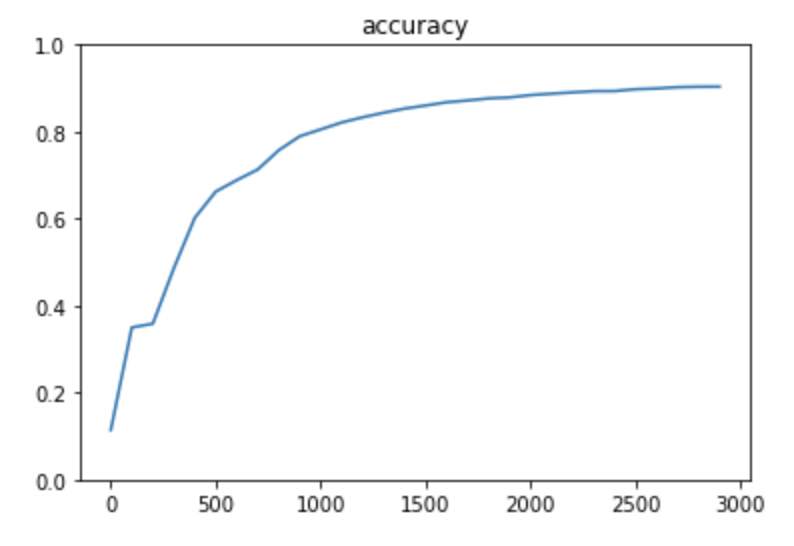
3層(Momentum)

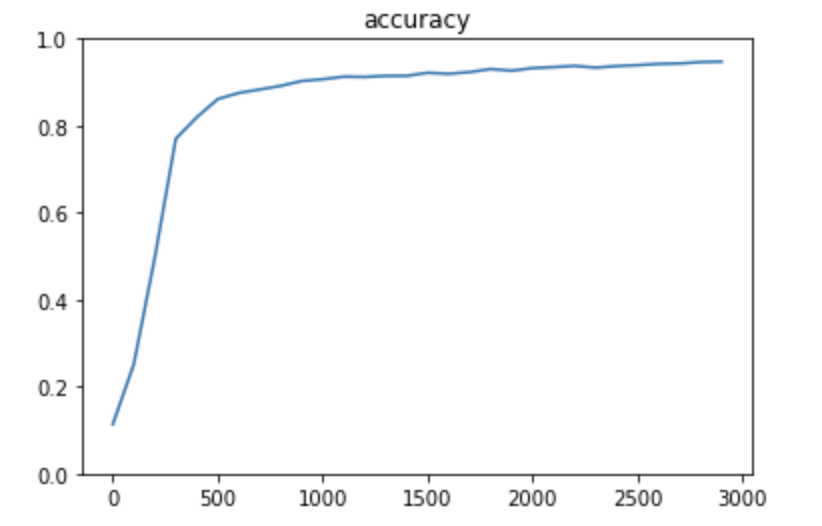
CNN(dropout_rate=0)

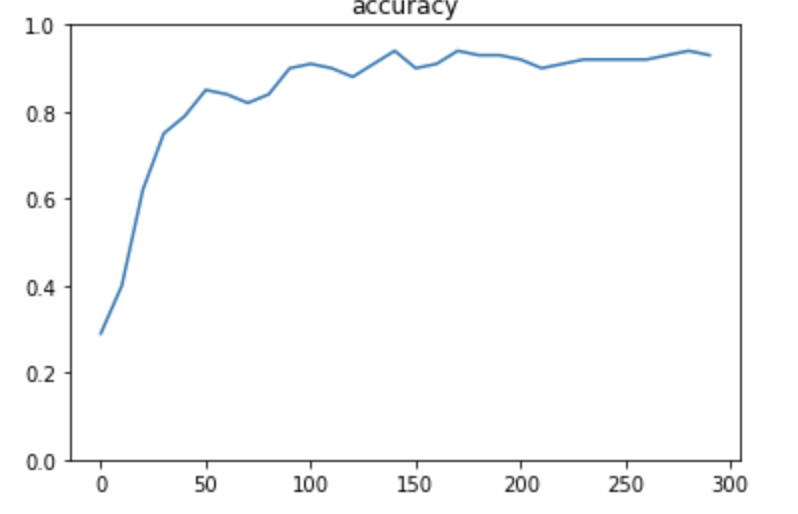
※ 中間層のサイズは、精度と速度のトレードオフ 中間層大きい：精度高い、速度遅い 中間層小さい：精度低い、速度早い

※ dropoutを実施しないと、精度は下がる

論文

論文から実装しよう

画像認識の最新モデルを実装するには?
・ VGG
・ AlexNet
・ GoogLeNet ・ Resnet
・ Yolo
→ 論文を見てみよう

※ ネットワークの形式や、リザルト、実装についても乗っているのでコツをつかむと論文から実務作業に落としこめる模様

※ VGGなどは有名なので、ブログでも解説があったりする

※ ライセンスには気をつけるべし

YOLO

物体認識の手法 → 実装まで公開されていて、githubにある

例題について

1 Inception module

GoogleNetの特徴としてInception moduleと呼ばれる復数のフィルタ郡により構成されたブロックが挙げられる。Inception moduleに関する記述として誤っているものはどれか

→ (a)が間違い。スパースなデータが増えているため

2 Auxiliary Less

GoogleNetｎのの特徴としてAuxiliary Lessの存在が挙げられる。Auxiliary Lossに関する記述といて間違っているものを選べ

→ (a)が間違い。Classifiersを増やすことによって計算量は増える

3 ResNet

深くモデルを設計出来なかった問題は？

→ (a) 勾配消失問題

4 ResNet

層をまたがる結合の名前

→ (a)。Identity mapping、いわゆるスキップコネクションのこと

5 Residual Brock

Residual Brockの導入によって期待されたもの

→ (a)。ブロックへの入力にこれ以上変換が必要ない場合は重みが0となり、小さな変換が求められる場合は対応する小さな変換をより見つけやすくなる

6 転移学習

転移学習の記載として誤ったものはどれか？

→ (あ) 。ワンショット学習というののはあるクラスにたいして画像を1枚用意して、特徴ベクトルを抽出する。特徴ベクトルが同じクラスであれば近い、離れていれば遠いということで判断する。転移学習の説明としては不当

7 一般物体検出アルゴリズム

一般物体検出アルゴリズムとして正しいものを選べ

→ (a) (b)は最大2つというのが間違い。必ず定義された２つの候補領域が生成される (c) 2つの誤差の単純和が間違い。2つの誤差の重み付けまで表現されている (d)出力についてはカテゴリのプラスの確率と２つの候補領域が出力される

確認テスト

GG, GoogleNet, ResNetの特徴をそれぞれ簡潔に述べよ

→ VGGについては2014からあるモデル 、単純なモデルの積み重ねになっているのでシンプルなモデル。ただしパラメータ数は多い → GoogleNetはinception moduleを使っている。次元削減やスパースなもので表現されるのが特徴 → ResNetはスキップコネクション：identity moduleを使って深い学習が出来る

Keras1

TensorFlowをラップする形式で、簡単に記載が可能 ただし、柔軟性はTensorFlowの方が高く細かいところで記載が必要であればTensorFlowを利用することも多い データ分析の実際の実務でも使うことは多く、TensorFlowの次くらいに利用者が多い

Python演習

線形回帰

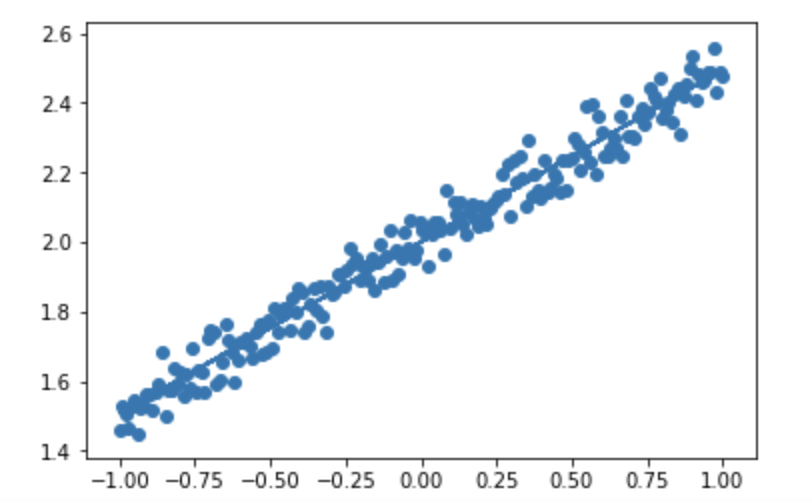
単純パーセプトロン

Epoch 30/30
4/4 [==============================] - 0s 3ms/step - loss: 0.2794
TEST
[[ True]
 [ True]
 [ True]
 [ True]]

Epoch 100/100
4/4 [==============================] - 0s 2ms/step - loss: 0.1640
TEST
[[ True]
 [ True]
 [ True]
 [ True]]

単純パーセプトロン(XOR)

...
model = Sequential()
model.add(Dense(input_dim=2, units=5,activation="relu"))
model.add(Dense(1))
model.add(Activation('sigmoid'))
model.summary()

model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
 
# トレーニング用入力 X と正解データ T
X = np.array( [[0,0], [0,1], [1,0], [1,1]] )
T = np.array( [[0], [1], [1], [0]] )
... 

Epoch 300/300
4/4 [==============================] - 0s 4ms/step - loss: 0.0213
TEST
[[ True]
 [ True]
 [ True]
 [ True]]

irisデータセット

花びらの大きさとかがく片のデータから花を分類したもの

relu

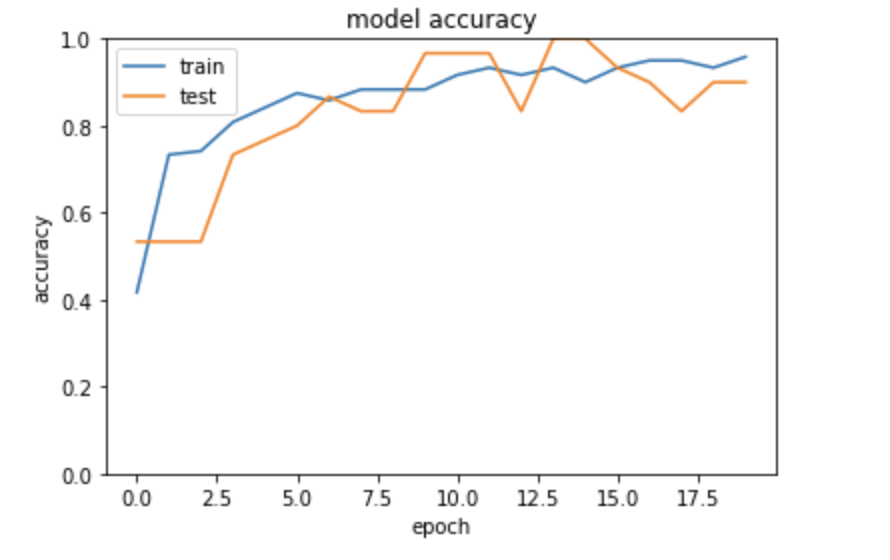
sigmoid

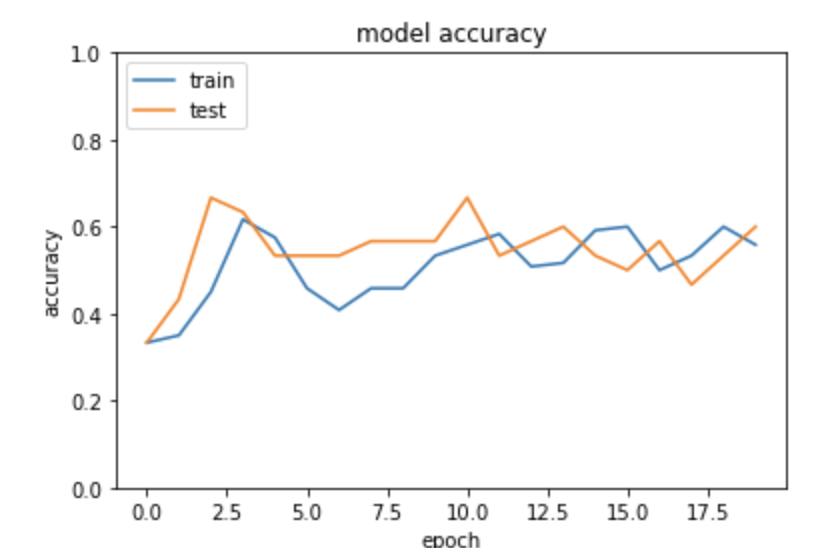
SGD(lr=0.1)

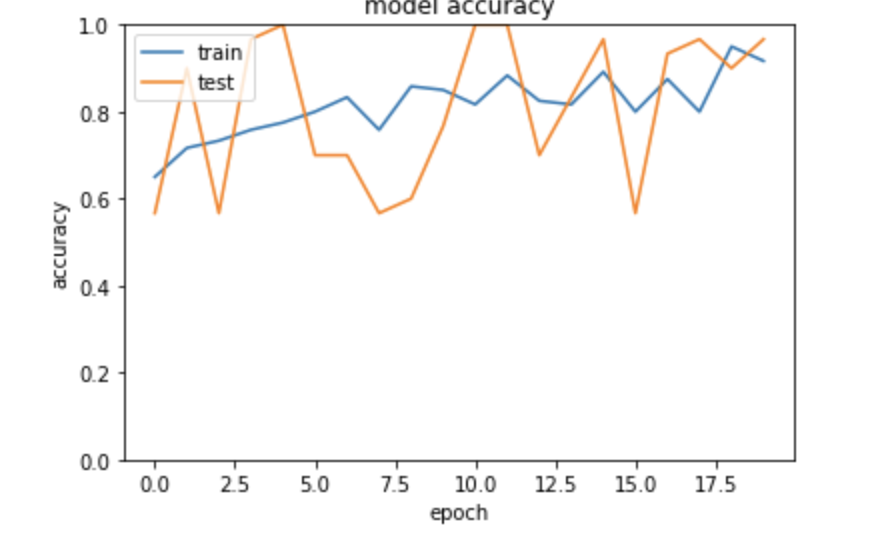
MNIST(NN)

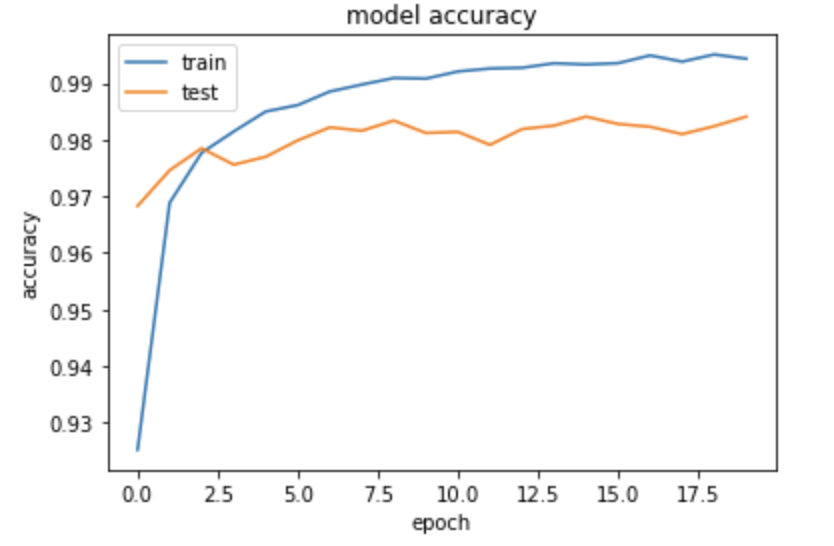
sparse_categorical_crossentropy

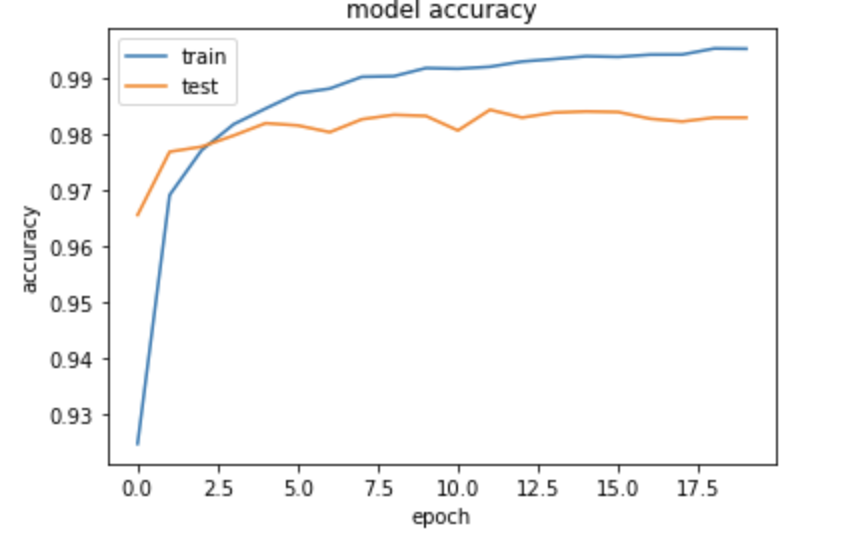
Adam(lr=0.01)

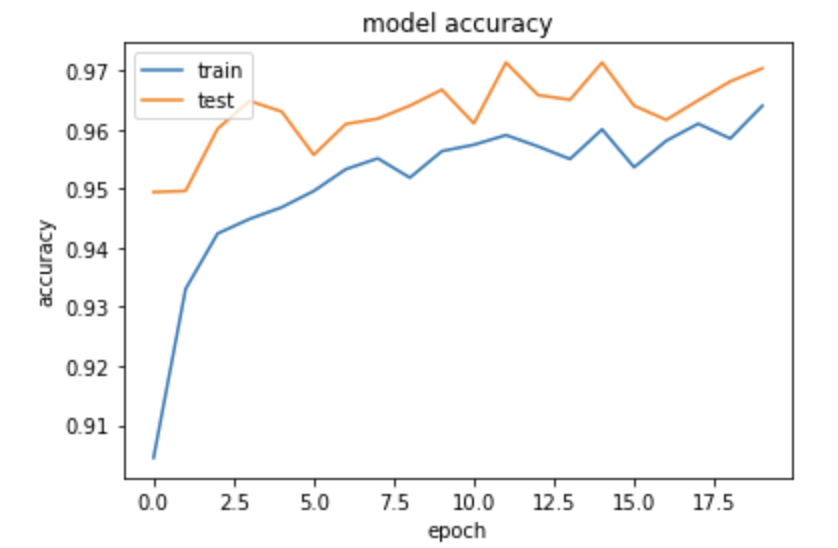
MNIST(CNN)

※途中で中断

cifar10(分類問題)

※途中で中断

RNN

Epoch 1/5
10000/10000 [==============================] - 16s 2ms/step - loss: 0.0638 - acc: 0.9450
Epoch 2/5
10000/10000 [==============================] - 15s 2ms/step - loss: 0.0017 - acc: 1.0000
Epoch 3/5
10000/10000 [==============================] - 15s 2ms/step - loss: 6.6395e-04 - acc: 1.0000
Epoch 4/5
10000/10000 [==============================] - 15s 2ms/step - loss: 4.0004e-04 - acc: 1.0000
Epoch 5/5
10000/10000 [==============================] - 15s 2ms/step - loss: 2.8125e-04 - acc: 1.0000

RNN(sigmoid)

Epoch 1/5
10000/10000 [==============================] - 17s 2ms/step - loss: 0.2476 - acc: 0.5392
Epoch 2/5
10000/10000 [==============================] - 16s 2ms/step - loss: 0.2294 - acc: 0.6658
Epoch 3/5
10000/10000 [==============================] - 16s 2ms/step - loss: 0.1137 - acc: 0.8800
Epoch 4/5
10000/10000 [==============================] - 16s 2ms/step - loss: 0.0149 - acc: 1.0000
Epoch 5/5
10000/10000 [==============================] - 16s 2ms/step - loss: 0.0011 - acc: 1.0000
Test loss: 0.00022750332874086856
Test accuracy: 1.0

RNN(tanh)

Epoch 1/5
10000/10000 [==============================] - 17s 2ms/step - loss: 0.0302 - acc: 0.9633
Epoch 2/5
10000/10000 [==============================] - 15s 2ms/step - loss: 3.5838e-04 - acc: 1.0000
Epoch 3/5
10000/10000 [==============================] - 15s 1ms/step - loss: 3.0595e-04 - acc: 0.9999
Epoch 4/5
10000/10000 [==============================] - 15s 2ms/step - loss: 7.6703e-04 - acc: 0.9993
Epoch 5/5
10000/10000 [==============================] - 15s 2ms/step - loss: 8.6655e-05 - acc: 1.0000
Test loss: 7.51769667030231e-05
Test accuracy: 1.0

RNN(adam)

Epoch 1/5
10000/10000 [==============================] - 17s 2ms/step - loss: 0.1151 - acc: 0.8616
Epoch 2/5
10000/10000 [==============================] - 16s 2ms/step - loss: 0.0153 - acc: 0.9971
Epoch 3/5
10000/10000 [==============================] - 16s 2ms/step - loss: 8.0843e-04 - acc: 0.9999
Epoch 4/5
10000/10000 [==============================] - 17s 2ms/step - loss: 2.0166e-04 - acc: 0.9998
Epoch 5/5
10000/10000 [==============================] - 14s 1ms/step - loss: 1.5597e-05 - acc: 1.0000
Test loss: 7.87067476825779e-06
Test accuracy: 1.0

強化学習

強化学習とは
長期的に報酬を最大化できるように環境のなかで行動を選択 できるエージェントを作ることを目標とする機械学習の一分野
→ 行動の結果として与えられる利益(報酬)をもとに、 行動を決定する原理を改善していく仕組みです。

確認テスト

強化学習が使えそうな分野 → オセロ、将棋などや自動運転、自動ゲーム操作など

探索と利用のトレードオフ

環境について事前に完璧な知識があれば、 最適な行動を予測し決定することは可能。 → どのような顧客にキャンペーンメールを送信すると、 どのような行動を行うのかが既知である状況。 →→ 探索と利用のトレードオフ 環境について事前に完璧な知識があれば、 最適な行動を予測し決定することは可能。 どのような顧客にキャンペーンメールを送信すると、 どのような行動を行うのかが既知である状況。

過去のデータで、ベストとされる行動のみを常に取り続ければ 他にもっとベストな行動を見つけることはできない。 → 探索が足りない状態 ↑ ↓ 未知の行動のみを常に取り続ければ、過去の経験が活かせない。 → 利用が足りない状態

強化学習の差分

強化学習と通常の教師あり、教師なし学習との違い

結論:目標が違う ・教師なし、あり学習では、データに含まれるパターンを見つけ出す およびそのデータから予測することが目標 ・強化学習では、優れた方策を見つけることが目標

行動価値観数

行動価値関数とは ・価値を表す関数としては、状態価値関数と行動価値関数の2種類がある ある状態の価値に注目する場合は、状態価値関数 状態と価値を組み合わせた価値に注目する場合は、行動価値関数

方策関数

方策関数とは 方策ベースの強化学習手法において、 ある状態でどのような行動を採るのかの確率を与える関数のことです。

方策勾配法について

方策反復法 方策をモデル化して最適化する手法

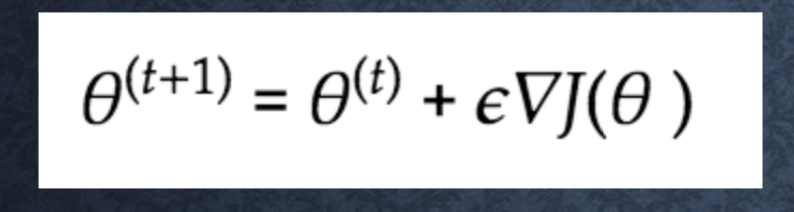
Jとは? 方策の良さ → 定義しないといけない

定義方法 ・平均報酬 ・割引報酬和 上記の定義に対応して、行動価値関数:Q(s,a)の定義を行い。 方策勾配定理が成り立つ。

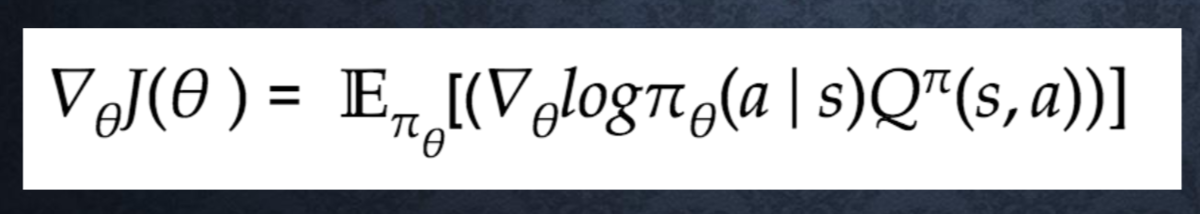
■方策勾配定理導出のポイント: 方策勾配定理は基本的には下記の2式から導出される

- 状態価値関数 v(s) = sum_a (π(a|s)Q(s,a))
- ベルマン方程式 Q(s,a) = sum_s’(P(s’|s,a)[r(s,a,s’) + γV(s’)]

DCGAN

敵対的ネットワークとCNNを使って、画像生成を行う →　実際には存在しないベッドルームの画像を生成したり

Leaky ReLU = 0以下が0じゃなくて、0.01 x になっている

Kaggle

10万人程度が参加している、機械学習のコンペサイト

※ 参加はfacebook id連携などで簡単にできる

※ これまでやってきた授業の内容で十分出来るようになっている

※ データセットの水増しとかテクニックは必要。Googleで調べると良い ※ 実際にやるとなるとKernelに関する議論などをまずは見てみる？

失敗談

• 一番最初つまずくのは、難しいのはどのコンテストに出るのか？
  • データセットが大きすぎてPCでは難しい

※ 最初はシングルモデルにしておいて、最終的にアンサンブル学習をさせるのが良いとのこと

実践につながるアウトプット

今は基本的に学習はKaggleのドキュメントを見ることが多い

【ラビットチャレンジ】 深層学習：その3 Day3まとめ

ラビットチャレンジ 深層学習：その3

前回からのおさらい

確認テスト

    サイズ5×5の入力画像を、サイズ3×3のフィルタで 畳み込んだ時の出力画像のサイズを答えよ。 なおストライドは2、パディングは1とする。

→ 3×3 画像

(5 + 2 * 1 - 3) / 2 + 1 = 3

Section1) RNN

• RNNとは?
  • 時系列データに対応可能な、ニューラルネットワークである。
• 時系列データとは？
• 時間的順序を追って一定間隔ごとに観察され，しかも相互に統計的依存関係が認められるようなデータの系列
  • 音声データ
  • テキストデータ
• 中間層が重要な意味を持ってくる

RNN全体像

u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
z[:,t+1] = functions.sigmoid(u[:,t+1])
np.dot(z[:,t+1].reshape(1, -1), W_out)
y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))

確認テスト

    RNNのネットワークには大きくわけて3つの重みが ある。1つは入力から現在の中間層を定義する際に かけられる重み、1つは中間層から出力を定義する際に かけられる重みである。 残り1つの重みについて説明せよ。

→ 中間層から次の中間層にかけられる重みがある

RNNの特徴とは

時系列モデルを扱うには、初期の状態と過去の時 間t-1の状態を保持し、そこから次の時間でのtを再 帰的に求める再帰構造が必要になる。

Jupyter演習

weight_init_std = 1

Xavier

He

Relu

tanh

    def d_tanh(x):
        return 1/(np.cosh(x) ** 2)

BPTT

BPTTとは? Backpropagation Through Time RNNにおいてのパラメータ調整方法の一種 ↓ 誤差逆伝播の一種

※ 人に教える → 誤差逆伝搬法を説明してみよう 計算結果(=誤差)から微分を逆算することで、不要な再帰的計算を避けて 微分を算出できる。

確認テスト

    連鎖律の原理を使い、dz/dxを求めよ。 
    z = t^2
    t = x +y

dz/dx = dz/dt * dt/dx dz/dt = 2t dt/dx=1

BPTTの数学的記述

確認テスト

    下図のy1をx・s0・s1・win・w・woutを用いて数式で表せ。 ※バイアスは任意の文字で定義せよ。 ※また中間層の出力にシグモイド関数g(x)を作用させよ。

↓

ビジネス事例

速度のためにGPUを使いたい → AWSやGCPを利用している

講師の人はスマートミラーを開発している

• 肌検出、異常検知
• キャラクターAI

などなど

※ ユーザーのためになるなら、AIを投入するのはやっていって良いのでは？

BTPPの全体像

パラメータの更新式

コード演習問題

※解説 RNNでは中間層出力 h{t}が過去の中間層出 力 h{t-1},.., h{1}に 依存する。 RNNにおいて損失関数を重 みWやUに関して偏微分す るときは、それを考慮する必 要があり、 dh{t}/dh_{t-1} = U であることに注意すると、過 去に遡るたびにUが掛けられ る。

Section2) LSTM

LSTM = Long short-term memory

RNNの課題

時系列を遡れば遡るほど、勾配が消失していく。 → 長い時系列の学習が困難。

勾配消失問題

誤差逆伝播法が下位層に進んでいくに連れて、勾配がどんど ん緩やかになっていく。 そのため、勾配降下法による、更新では下位層のパラメータ はほとんど変わらず、訓練は最適値に収束しなくなる。

解決策として活性化関数を調整する → シグモイド関数など → 0 ~ 1の間を緩やかに変化する関数で、ステップ関数ではON/OFFしかない 状態に対し、信号の強弱を伝えられるようになり、予想ニューラルネットワーク普 及のきっかけとなった。 → 大きな値では出力の変化が微小なため、勾配消失問題を引き起こすがあった

確認テスト

シグモイド関数を微分した時、入力値が0の時に最大値 をとる。その値として正しいものを選択肢から選べ。

→ 0.25

勾配爆発

勾配が、層を逆伝播するごとに指数関数的に大きくなっていく

演習チャレンジ

RNNや深いモデルでは勾配の消失または爆発が起こる傾向がある。勾配爆発を防ぐために勾配のクリッピングを行うという 手法がある。具体的には勾配のノルムがしきい値を超えたら、勾配のノルムをしきい値に正規化するというものである。以下は勾配のクリッピングを行う関数である。
(さ)にあてはまるのはどれか。

→ (1) gradient * rate

勾配のノルムがしきい値より大きいときは、勾配のノルムをしきい値に正規化するので、クリッピングした勾配は、勾配×(し きい値/勾配のノルム)と計算される。つまり、gradient * rateである。

つまり、delta_t = delta_t.dot(U)となる。

CEC

勾配消失および勾配爆発の解決方法として、勾配が、1であれば解決できる。

課題

入力データについて、
時間依存度に関係なく重みが一律である。
→ ニューラルネットワークの学習特性が無いということ

入力ゲート・出力ゲート

入力・出力ゲートの役割とは?

入力・出力ゲートを追加することで、 それぞれのゲートへの入力値の重みを、 重み行列W,Uで可変可能とする。

→ CECの課題を解決

忘却ゲート

LSTMの現状(CEC, 入出力ゲートのみ) CECは、過去の情報が全て保管されている → 過去の情報が要らなくなった場合、削除することはできず、保管され続ける

過去の情報が要らなくなった場合、そのタイミングで情報を忘却する機能が必要
→ 忘却ゲートの誕生

確認テスト

以下の文章をLSTMに入力し空欄に当てはまる単語を予測したいとする。 文中の「とても」という言葉は空欄の予測において なくなっても影響を及ぼさないと考えられる。 このような場合、どのゲートが作用すると考えられるか。
「映画おもしろかったね。ところで、とてもお腹が空いたから何か____。」

→ 忘却ゲート

演習チャレンジ

以下のプログラムはLSTMの順伝播を行うプログラムである。ただし_sigmoid関数は要素ごとにシグモイド関数を作用 させる関数である。
(け)にあてはまるのはどれか。

→ 3

新しいセルの状態は、計算されたセルへの入力と1ステップ前のセルの状態に入力ゲート、忘却ゲートを掛けて足し合 わせたものと表現される。つまり、input_gate * a + forget_gate * prev_cとなる

のぞき穴結合

CECの保存されている過去の情報を、 任意のタイミングで他のノードに伝播させたり、 あるいは任意のタイミングで忘却させたい。 CEC自身の値は、ゲート制御に影響を与えていない

• 覗き穴結合とは?
  • CEC自身の値に、重み行列を介して伝播可能にした構造。

Section3) GRU

LSTMの課題 → LSTMでは、パラメータ数が多く、計算負荷が高くなる問題があった → GRUで解決する

GRUとは？

Gated Recurrent Unit 従来のLSTMでは、パラメータが多数存在していたため、計算負荷が大きかった。しかし、GRUでは、そのパラメータを大幅に削減 し、精度は同等またはそれ以上が望める様になった構造。 → 構造を変えたLSTM。大幅に構造が変わっている

※ 必ずしもGRUがLSTMの上位互換ではない

確認テスト

LSTMとCECが抱える課題について、それぞれ簡潔に述べよ。

LSTMはパラメータ数が多く、計算負荷が高い CECは勾配が1になるので、最適なパラメータを学習するという概念がなくなってしまう

演習チャレンジ

GRU(Gated Recurrent Unit)もLSTMと同様にRNNの一種であり、単純なRNNにおいて問題となる勾配消失 問題を解決し、長期的な依存関係を学習することができる。LSTMに比べ変数の数やゲートの数が少なく、より単純 なモデルであるが、タスクによってはLSTMより良い性能を発揮する。以下のプログラムはGRUの順伝播を行うプログラム である。ただし_sigmoid関数は要素ごとにシグモイド関数を作用させる関数である。
(こ)にあてはまるのはどれか。

→ 4

新しい中間状態は、1ステップ前の中間表現と計算された中間表現の線形和で表現される。つまり更新ゲートzを用 いて、(1-z) * h + z * h_barと書ける。

確認テスト

LSTMとGRUの違いを簡潔に述べよ

→ パラメータの数がLSTMの方が多い。そのためGRUの方が実行速度の面で有利 どっちがどのタスクで有利かはケースバイケース

Section4) 双方向RNN

双方向RNN 過去の情報だけでなく、未来の情報を加味することで、精度を向上させるためのモデル

演習チャレンジ

以下は双方向RNNの順伝播を行うプログラムである。順方向については、入力から中間層への重みW_f, 一ステッ プ前の中間層出力から中間層への重みをU_f、逆方向に関しては同様にパラメータW_b, U_bを持ち、両者の中 間層表現を合わせた特徴から出力層への重みはVである。_rnn関数はRNNの順伝播を表し中間層の系列を返 す関数であるとする。(か)にあてはまるのはどれか

→ 4 np.concatenate([h_f, h_b[::-1]], axis=1)

双方向RNNでは、順方向と逆方向に伝播したときの中間層表現をあわせたものが特徴量となるので、 np.concatenate([h_f, h_b[::-1]], axis=1)である。

※ np.concatenateは配列の結合。axisに指定した軸方向に新しい要素を追加するため、axisによっては配列の形状が噛み合わないとエラーが発生します。(1次元配列ではaxis=1以上はエラー)

Section5) Seq2Seq

• Seq2Seqとは？
  • Encoder-Decoderモデルの一種
• Seq2seqの具体的な用途とは?
  • 機械対話や、機械翻訳などに使用

Encoder RNN

ユーザーがインプットしたテキストデータを、 単語等のトークンに区切って渡す構造

• Taking : 文章を単語等のトークン毎に分割し、トークンご とのIDに分割する。
• Embedding : IDから、そのトークンを表す分散表現ベクトル に変換。
• Encoder RNN:ベクトルを順番にRNNに入力していく

vec1をRNNに入力し、hidden stateを出力。 このhidden stateと次の入力vec2をまたRNNに入力してき たhidden stateを出力という流れを繰り返す。 最後のvecを入れたときのhidden stateをfinal stateとし てとっておく。このfinal stateがthought vectorと呼ばれ、 入力した文の意味を表すベクトルとなる

Decoder RNN

システムがアウトプットデータを、 単語等のトークンごとに生成する構造

確認テスト

下記の選択肢から、seq2seqについて説明しているものを選べ。
(1)時刻に関して順方向と逆方向のRNNを構成し、それら2つの中間層表現を特徴量として利用 するものである。
(2)RNNを用いたEncoder-Decoderモデルの一種であり、機械翻訳などのモデルに使われる。
(3)構文木などの木構造に対して、隣接単語から表現ベクトル(フレーズ)を作るという演算を再帰的に行い(重みは共通)、文全体の表現ベクトルを得るニューラルネットワークである。
(4)RNNの一種であり、単純なRNNにおいて問題となる勾配消失問題をCECとゲートの概念を 導入することで解決したものである。

→ 2

演習チャレンジ

機械翻訳タスクにおいて、入力は複数の単語から成る文(文章)であり、それぞれの単語はone-hotベクトルで表 現されている。Encoderにおいて、それらの単語は単語埋め込みにより特徴量に変換され、そこからRNNによって (一般にはLSTMを使うことが多い)時系列の情報をもつ特徴へとエンコードされる。以下は、入力である文(文 章)を時系列の情報をもつ特徴量へとエンコードする関数である。ただし_activation関数はなんらかの活性化関 数を表すとする。
(き)にあてはまるのはどれか。

→ 1

単語wはone-hotベクトルであり、それを単語埋め込みにより別の特徴量に変換する。これは埋め込み行列E を用いて、E.dot(w)と書ける。

HRED

Seq2seqの課題 → 一問一答しかできない

問に対して文脈も何もなく、ただ応答が行われる 続ける。

HREDとは？ → 過去 n-1 個の発話から次の発話を生成する

Seq2seqでは、会話の文脈無視で、 応答がなされたが、HREDでは、 前の単語の流れに即して応答されるため、 より人間らしい文章が生成される。

HRED = Seq2Seq+ Context RNN

Context RNN → Encoder のまとめた各文章の系列をまとめて、これ までの会話コンテキスト全体を表すベクトルに変換する構造。 → 過去の発話の履歴を加味した返答をできる

VHRED

HREDに、VAEの潜在変数の概念を追加したもの。 → HREDの課題を、 VAEの潜在変数の概念を追加することで解決した構造。

※ 毎回同じ答えしか出ないというHREDの課題を解決するもの

確認テスト

seq2seqとHRED、HREDとVHREDの違いを簡潔に述べよ。

Seq2seqとHREDの違い → 1問1答しか出来ない構造を改修したのがHRED HREDとVHREDの違い → 同じ文脈だと毎回同じ答えしか出ないHREDを改修したのがVHRED

AE(オートエンコーダ)

オートエンコーダとは？ → 教師なし学習の一つ。そのため学習時の入力ではた訓練データのみで教師データは使用しない

オートエンコーダ具体例

MNISTの場合、28x28の数字の画像を入れて、 同じ画像を出力するニューラルネットワークということ

オートエンコーダ構造説明

入力データから潜在変数zに変換するニューラルネットワークをEncoder 逆に潜在変数zをインプットとして元画像を復元するニューラルネットワーク をDecoder。

メリット → 次元削減が行えること

牽引企業

• AWS
  • 使いやすい
• GCP
  • TPUとかのせいでNVIDIA-GPUが使えてない
  • 若干の使いにくさ

※ TensorFlowについては講師の人も勉強している

• Preferred Networks
• NVIDIA
• TOYOTA
  • 自動運転の分野

VAE

通常のオートエンコーダーの場合、 何かしら潜在変数zにデータを押し込めているものの、 その構造がどのような状態かわからない。 → VAEはこの潜在変数zに確率分布z∼N(0,1)を仮定したもの。

VAEは、データを潜在変数zの確率分布という構造に押し込め ることを可能にします。

確認テスト

VAEに関する下記の説明文中の空欄に当てはまる言葉を答えよ。
自己符号化器の潜在変数に____を導入したもの。

→ 確率分布

Section6) word2vec

課題:RNNでは、単語のような可変長の文字列をNNに与えることはできない。 → 固定長で単語を表す必要がある

学習データからボキャブラリを作成 わかりやすく7語のボキャブラリを作成したら 本来は、辞書の単語数だけできあがる

Ex) I want to eat apples. I like apples.
{apples,eat,I,like,to,want}

One-hot ベクトル

Applesを入力する場合は、入力層には以下のベクトルが入力される。 → 本来は、辞書の単語数だけone-hotベクトルができあがる。

    1...apples 
    0...eat 
    0...I 
    0...like 
    0...to
    …

word2vecのメリット

大規模データの分散表現の学習が、現実的な計算速度とメモリ量で実現可能にした。

X:ボキャブラリ×ボキャブラリだけの重み行列が誕生。
○:ボキャブラリ×任意の単語ベクトル次元で重み行列が誕生。

Section7) Attention Mechanism

課題: seq2seq の問題は長い文章への対応が難しいです。 seq2seq では、2単語でも、100単語でも、固定次元ベクトルの中に入力しなければならない。

解決策: 文章が長くなるほどそのシーケンスの内部表現の次元も大きくなっていく、 仕組みが必要になる → Attention Mechanism → 「入力と出力のどの単語が関連しているのか」 の関連度を学習する仕組み。

具体例

確認テスト

RNNとword2vec、seq2seqとseq2seq+Attention Mechanismの違いを簡潔に述べよ。

word2vecはwordに対して重みをつけて、現実的な処理速度にしている。RNNはボキャブラリ×ボキャブラリでデータを処理する seq2seqに比べてAttention Mechanismは長い文章を入れたときにでも翻訳として成り立ちやすい。入出力間の重要度が学習に対して効いてくる

演習チャレンジ

 以下は再帰的ニューラルネットワークにおいて構文木を入力として再帰的に文全体の表現ベクトルを得るプログラムである。ニューラルネットワークの重みパラメータはグローバル変数として定義してあるものとし、_activation関数はなんらかの活性化関数であるとする。木構造は再帰的な辞書で定義してあり、rootが最も外側の辞書であると仮定する。
(く)にあてはまるのはどれか

→ 2 W.dot(np.concarenate([left, right))

実務経験をつむ

※ 経験をつむにはできるだけデータが多い企業で働いたほうがよい データを使ったモデルがどうサービスとして使えるかも観点

【ラビットチャレンジ】 深層学習：その2 Day2まとめ

ラビットチャレンジ 深層学習：その2

講義全体の流れ

テーマは CNN

1. 入力層に値を入力
2. 重み、バイアス、活性化関数で計算しながら値が伝わる
3. 出力層から値が伝わる
4. 出力層から出た値と正解値から、誤差関数を使って誤差を求める
5. 誤差を小さくするために重みやバイアスを更新する
6. 1〜5の操作を繰り返すことにより、出力値を正解値に近づけていく

誤差逆伝播法の復習

計算結果(=誤差)から微分を逆算することで、不要な再帰的計算を避けて 微分を算出できる

確認テスト

連鎖律の原理を使い、dz/dxを求めよ。

Section1 勾配消失問題について

勾配消失問題

勾配がなくなることにより、誤差逆伝搬で値が更新されなくなる

シグモイド関数：大きな値では出力の変化が微小なため、勾配消失問題を引き起こす事 があった。

確認テスト

シグモイド関数を微分した時、入力値が0の時に最大値をとる。その値 として正しいものを選択肢から選べ。

f(u)’ = (1 -1 sigmoid(u)) * sigmoid(u) sigmoid(0) = 0.5のため、 微分値の最大は 0.25 となる

勾配消失のビジョン

解決法

• 活性化関数の選択
• 重みの初期値設定
• バッチ正規化

活性化関数：ReLU関数

今最も使われている活性化関数 勾配消失問題の回避とスパース化に貢献することで良い成果をもたらし ている。

def relu(u):
  return np.maximum(0,x)

重みの初期値設定- Xavier

初期値を設定する際の活性化関数

• ReLU関数
• シグモイド(ロジスティック)関数
• 双曲線正接関数

初期値の設定方法

→ 重みの要素を、前の層のノード数の平方根で除算した値

重みの初期値設定- He

初期値を設定する際の活性化関数

• ReLU関数

初期値の設定方法 → 重みの要素を、前の層のノード数の平方根で除算した値に対し√2をかけ合わせた値

確認テスト

重みの初期値に0を設定すると、どのような問題が 発生するか。簡潔に説明せよ。

→ すべての値が同じ値で伝わるためパラメータのチューニングが行われなくなる

バッチ正規化

• バッチ正規化とは?
  • ミニバッチ単位で、入力値のデータの偏りを抑制する手法
• バッチ正規化の使い所とは?
  • 活性化関数に値を渡す前後に、バッチ正規化の処理を孕んだ層を加える

確認テスト

一般的に考えられるバッチ正規化の効果を2点挙げよ。

1. 計算の高速化
2. 勾配消失が起きづらくなる

バッチ正則化の数学的記述

※ 数式から意味を読み取ってほしい ※ 適切に実装出来るようになってほしい

Jupyter

2_2_1_vanishing_gradient → sigmoid - gaussでは勾配消失問題が出ている → ReLUでは起きていない → 初期値を工夫しても起きづらくなっている(Xavier, He)

※ 結果のグラフ化、見える化が大事。感覚をつかみやすい

ReLU / Xavier

Sigmoid / He

データについて

• 例）顔画像がほしい
  • どうやって集めるか？
  • サービスに結びつける。API提供など
• 国内と海外の事情について
  • 国内は法整備がルーズじゃないか？
    • 今のうちに色々やっておくほうが良さそう
  • 国内のクライアントさんが持っているデータが少ない

Section2 学習率最適化手法について

深層学習の目的：誤差を最小化するパラメータを発見すること → 勾配降下法を利用してパラメータを最適化

    学習率の復習
    学習率の値が大きい場合
    ・最適値にいつまでもたどり着かず発散してしまう。
    
    学習率の値が小さい場合 
    ・発散することはないが、小さすぎると収束するまでに時間がかかっ てしまう。
    ・大域局所最適値に収束しづらくなる

初期の学習率設定方法

• 初期の学習率を大きく設定し、徐々に学習率を小さくしていく
• パラメータ毎に学習率を可変させる

モメンタム

学習率最適化手法の一つ

モメンタム	勾配降下法
誤差をパラメータで微分したもの と学習率の積を減算した後、現在 の重みに前回の重みを減算した値 と慣性の積を加算する	誤差をパラメータで微分したも のと学習率の積を減算する

モメンタムのメリット

• 局所的最適解にはならず、大域的最適解となる
• 谷間についてから最も低い位置(最適値)にいくまでの時間が早い

確認テスト

モメンタム・AdaGrad・RMSPropの特徴を それぞれ簡潔に説明せよ

モメンタム：最も低い位置(最適値)にいくまでの時間が早い AdaGram：最適値に近づきやすい RMSProp：パラメータの調整が少ない

※ 学習率最適化手法 を利用して学習率を最適化

AdaGram

学習率最適化手法の一つ

AdaGrad	勾配降下法
誤差をパラメータで微分したもの と 再定義した学習率の積を減算する	誤差をパラメータで微分したも のと学習率の積を減算する

AdaGramのメリット・デメリット

• 勾配の緩やかな斜面に対して、最適値に近づける
• 学習率が徐々に小さくなるので、鞍点問題を引き起こす事があった

※ 鞍点：鞍点（あんてん、saddle point）は、多変数実関数の変域の中で、ある方向で見れば極大値だが別の方向で見れば極小値となる点である。 鞍部点、峠点とも言う。微分可能な関数については極値を取らない停留点とも言う。

RMSProp

学習率最適化手法の一つ

RMSProp	勾配降下法
誤差をパラメータで微分したもの と 再定義した学習率の積を減算する	誤差をパラメータで微分したも のと学習率の積を減算する

RMSPropのメリット

・局所的最適解にはならず、大域的最適解となる。 ・ハイパーパラメータの調整が必要な場合が少ない

Adam

学習率最適化手法の一つ → ちゃんと見るのは時間がかかる…

• Adamとは?
  • モメンタムの、過去の勾配の指数関数的減衰平均
  • RMSPropの、過去の勾配の2乗の指数関数的減衰平均 上記をそれぞれ孕んだ最適化アルゴリズムである。
• Adamのメリットとは?
  • モメンタムおよびRMSPropのメリットを孕んだアルゴリズムである

Jupiter演習

• SGD

• モメンタム

※ パラメータとしては0.5〜0.9くらいしか設定されているのを見たことがない

    # 慣性
    momentum = 0.9

• MomentumをもとにAdaGradを作ってみよう

    # 変更しよう  
    if i == 0:
      h[key] = np.full_like(network.params[key], 1e-4)        
    else:
      h[key] += np.square(grad[key])        
    h[key] = momentum * h[key] - learning_rate * grad[key]
    network.params[key] -= learning_rate * grad[key] / (np.sqrt(h[key]))

• RSMProp

• Adam(実装例)

シンギュラリティ

• 体内チップの話
• 日本の全能学会
  • ドラえもんのようなものを作ったりしている
• AIには欲が無い
• 最先端の論文を見て、シンギュラリティに近づいているか？などを考えると良いモチベーションになる

Section3 過学習について

テスト誤差と訓練誤差とで学習曲線が乖離すること → 特定の訓練サンプルに対して、特化して学習する

原因

• パラメータの数が多い
• パラメータの値が適切でない
• ノードが多い

ネットワークの自由度(層数、ノード 数、パラメータの値etc...)が高い → NNにおける課題

正則化

ネットワークの自由度(層数、ノード数、パラメータの値etc...)を制約すること → 正則化手法を利用して過学習を抑制する

正則化手法について

• L1正則化、L2正則化
• ドロップアウト

確認テスト

リッジ回帰の特徴として正しいものはどれか？

→ ハイパーパラメータに大きな値を設定すると、すべての重みが限りなく0に近づく

※ 線形回帰となる ※ 誤差関数に正則化項を与える

Weight decay(荷重減衰)

過学習の原因：重みが大きい値をとることで、過学習が発生することがある

過学習の解決策：誤差に対して、正則化項を加算することで、重みを抑制する

L1、 L2正則化

確認テスト

L1正則化を表しているグラフは どちらか

L1はLasso推定 → スパース推定される

L2は計算は多くなるが、最適化としては良い結果を出している

例題チャレンジ

※ L2パラメータ正則化 L2ノルムは、 ||param||^2　であり、その勾配(微分値)が誤差の勾配に加えられる。

→  2 * paramであるが、係数2は正則化の係数に吸収されても変わらないので param になる
→ (4) が答え

※ L1パラメータ正則化 L1ノルムは、|param|なのでその勾配が誤差の勾配に加えられる → sign(param) となる → (3)が答え

※ データ集合の拡張

→ (3) が答え

ドロップアウト

過学習の課題 → ノードの数が多いというのがある

ドロップアウトとは? → ランダムにノードを削除して学習させること → メリットとしてデータ量を変化させずに、異なるモデルを学習させていると解釈できる

※ TensorFlowでの実装などはブラックボックス… → ただし、層ごとにノードの閾値を設けたりしている？ 効果は高い

ソースコード演習

overfitting

Weight decay(L2)
weight_decay_lambda = 0.1

Weight decay(L2)
weight_decay_lambda = 0.4

weight_decay_lambda が小さい → 過学習が抑制されない weight_decay_lambdaが大きい → 過学習はされないが精度が出ない

Weight decay(L1)

Jupyter演習(Dropout)

※ クラスをよく利用する。再利用性が高い またライブラリも利用します(Chainerなど)

Dropout

Dropout(ratio=0.4)

Dropout(ratio=0.02)

Dropout(Adam, ratio=0.15)

Dropout + L1

自分で課題設定

検索について → 日本語で検索はあまりやらない → 翻訳家の質によるため… 英語だとそこは問題にならない

論文について → 論文発表やそれぞれの論文の関連など、時系列を意識したほうが良い → 論文、参考文献、関連書籍をインプットしていくときに

課題設定、目的を自分でちゃんと言語化出来るようにしたい → 他人に説明出来るくらいには

畳み込みニューラルネットワークについて

画像の分野でソリューションを提供している → 音声や時系列データにも応用は可能

LeNet : CNNの出処

畳み込み層

畳み込み層では、 画像の場合、縦、横、チャンネルの3次元 のデータをそのまま学習し、次に伝えるこ とができる。

結論:3次元の空間情報も学習できるような 層が畳み込み層である。

※ 全結合NNでは空間情報は明確には保持しない

畳み込みの概念

• フィルターをかける
• バイアスを足し合わせる

→ 出力画像が出せる

パディング

入力画像と出力画像を合致させるために入力画像に固定データで枠をつけるイメージ

ストライド

いわゆるずらす幅

チャンネル

CNNのミソ

全結合層のデメリット 画像の場合、縦、横、チャンネルの3次元データだが、 1次元のデータとして処理される。 → RGBの各チャンネル間の関連性が、 学習に反映されないということ。

Jupyter演習

im2col → 多次元データを２次元化する メリットは、行列計算に落とし込むことで多くのライブラリを活用できる

col2im → ２次元データを多次元化する ただし、元の形に戻すためにはshapeが必要

# im2colの処理確認
input_data = np.random.rand(2, 1, 4, 4)*100//1 # number, channel, height, widthを表す
print('========== input_data ===========\n', input_data)
print('==============================')
filter_h = 3
filter_w = 3
stride = 1
pad = 0
col = im2col(input_data, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad)
print('============= col ==============\n', col)
print('==============================')
# col2imの処理確認
output_data = col2im(col, input_shape=input_data.shape, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad)
print('============= output_data ==============\n', output_data)

プーリング層

maxプーリングとavgプーリングがある → それぞれ領域での最大値を選択したり平均を選択したりする

確認テスト

サイズ6×6の入力画像を、サイズ2×2のフィルタで 畳み込んだ時の出力画像のサイズを答えよ。 なおストライドとパディングは1とする。

→ 7×7

※ (H+2P - FH) / S + 1 = (6 + 2×1 - 2) / 1 + 1 = 7

Jupyter演習

Simple Convolution Network

シラバス

書籍「Deep Learning」

認定プログラムはシラバスの項目を網羅＆実装に不足部分を追加

※ 試験前にこのまとめは良く読んで復習しておく

応用数学

・講義の内容を理解していればシラバスの範囲(筆記試験)は問題ありません。 ・誤差逆伝播法で用いる偏微分などはシラバスには含まれませんが追加。

機械学習

・特別な技術ではなく一般的な話のまとめ。

NN

・Day1の講義で扱った最も基本的 な内容です。基本だけに重要。予習資料 を手打ち、手計算で繰り返しましょう。

正則化

・講義では正則化の流れを最もスタンダードな手法を用いて演習しました。 ・講義で扱っていない内容は演習問題のキーワードやシラバスから自身での まとめ学習をしてください。(9Action 検索力向上で後述)

※ CNNが最重要

Section5 最新のCNN

AlexNet

AlexNetとは2012年に開かれた画像認識コンペティション 2位に大差をつけて優勝したモデルである。 AlexNetの登場で、ディープラーニングが大きく注目を集 めた。

• モデルの構造
  • 5層の畳み込み層およびプーリング層な ど、それに続く3層の全結合層から構成 される。
• 過学習を防ぐ施策
  • サイズ4096の全結合層の出力にドロップアウトを使用してい る

検索力の向上

英語で検索しよう

自分で課題を設定しよう

• 訴求
  • 公営競技の予想AIを制作したい。
• 課題(よくある)
  • 手元にデータが無い

「クローラーを作ってみる」という課題が設定できる!!

【ラビットチャレンジ】深層学習：Day1 まとめ

ラビットチャレンジ 深層学習：その1

講師紹介

• Noberaの人

Day1

• NN

9 ROOP

• 基礎を反復

9 STORY

• 多角的に全体像を把握

フレームワークや牽引企業も紹介

9 ACTION

• 終了課題
• 制作課題

人に教える。言語化するは重要なこと

ニューラルネット全体像

• エンジニアが一番注目すべきは中間層

※ 例は動物を分類する 入力層の中で、何が重要なのかを頭で理解できるかどうかがポイント

確認テスト

• Q: ディープラーニングは結局何をやろうとしているか？ 2行以内で述べよ
  • A: ある入力に対応する出力を学習し、未知の入力に対して適切な出力を提供する処理を提供する

答えの:例：誤差を最小化するパラメータを発見すること

値の最適化の最終目的：３ 重み，４ バイアス

全体像：パラメータなど

W: 重み b: バイアス

↑ ２つ合わせて wで表す

ニューラルネットワーク(NN)で出来ること

• 回帰
  • 結果予想
  • ランキング
• 分類
  • 猫写真の判別
  • 手書き文字認識
  • 花の種類分類

※ 最終課題はアイリスデータの分類

実用例

• 自動売買(トレード)
• チャットボット
• 翻訳
• 音声解釈
• 囲碁、将棋AI

※ 音声データは実用化するために集める量が現実的ではない 既存ライブラリはAPIで提供されているものを利用するのが良い

Section 1 入力層から中間層

• 入力
• 重み
• バイアス
• 総入力
• 出力
• 活性化関数

確認テスト1

動物分類の実例を入れよ

確認テスト2

u = x1w1 + x2w2 + x3w3…. + b の数式をPythonで書け

u1 = np.dot(x, W1) + b1

確認テスト3

1-1のファイルから 中間層の出力を定義しているソースを抜き出せ

    # 中間層出力
    z = functions.relu(u)
    print_vec("中間層出力", z)

Jupyter演習

入力 [01,0.2] バイアス 0.5

活性化関数 : relu

numpy使い方

np.zeros(2) → zero初期化

np.ones(2) → 1で初期化

np.random.rand(2) → ランダム値(0〜1)

np.random.randint(5, size=(2)) → ランダム値(任意の整数: ここでは5)

Section2 活性化関数導入

活性化関数

ニューラルネットワークにおいて、次の層への出力の大きさを決める 非線形 の関数 入力値の値によって、次の層への信号の on/off や強弱を定める働きを持つ

確認テスト(線形/非線形)

中間層用の活性化関数

• ReLU関数
• シグモイド(ロジスティック)関数
• ステップ関数

※ステップ関数は微分すると0になるので、使われない 人間の脳を目指すみたいな話だったのにステップ関数は機械的になる ↓ ※シグモイドは使われるが、課題も多い 大きな値では出力の変化が微小なため、勾配消失問題を引き起こすことがあった ↓ ※ReLUは今もっとも使われている活性化関数 勾配消失問題の回避とスパース化に貢献することで良い成果をもたらしている

全結合NN - 単相複数ノード

活性化関数の効果で一部の出力は弱く、一部は強く伝搬される

確認テスト

中間層出力zを求める箇所はソースコード中のどこか？ z = functions.sigmoid(u)

functionsはなにか？ functions.pyというファイルに定義されている関数群のモジュール

Section3 出力層

人間が分かる形の出力にしたい → そのため出力層の処理もかなり重要

※ ねずみの確率100％みたいな出力は疑ってかかったほうが良い

誤差関数

誤差関数はどこで使う？ 出力データと訓練データとの差を見るときに使う

確認テスト

1. なぜ2乗しているのか？

   → マイナス値を出さないため

2. なぜ 1/2 しているのか？

   → 微分したときに計算しやすいため

出力層用の活性化関数

• ソフトマックス関数
• 恒等写像
• シグモイド(ロジスティック)関数

※ 中間層と何が違うのか？ 【値の強弱】 中間層：しきい値の前後で信号の強弱を調整 出力層：信号の大きさ(比率)はそのままに変換 【確率出力】 分類問題の場合、出力層の出力は 0 ~ 1 の範囲に限定し、総和を1とす る必要がある

出力層の種類 - 組み合わせ

※この組み合わせは重要

	回帰	二値分類	多クラス分類
活性化関数	恒等写像	シグモイド関数	ソフトマックス関数
誤差関数	二乗誤差	交差エントロピー	交差エントロピー

数式とコード

シグモイド関数

    def sigmoid(x):
      return 1/(1 + np.exp(-x))

ソフトマックス関数(確認テスト込)

    def softmax(x): ①
      if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) /np.sum(np.exp(x), axis=0) 
        return y.T
      x = x - np.max(x) # オーバーフロー対策 
      return np.exp(x) ② / np.sum(np.exp(x)) ③

二乗誤差

    def mean_squared_error(d, y):
      return np.mean(np.square(d - y)) / 2

交差エントロピー(確認テスト込)

    def cross_entropy_error(d, y):  ①
      if y.ndim == 1:
        d = d.reshape(1, d.size)
        y = y.reshape(1, y.size)
        # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
        if d.size == y.size:
          d = d.argmax(axis=1) 
          batch_size = y.shape[0]
      return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size ②

Section4 勾配降下法

深層学習の目的

学習を通して誤差を最小にするネットワークを作成すること → 誤差E(w)を最小化するパラメータwを発見すること

確認テスト

勾配降下法の該当するソースコードを探せ

    grad = backward(x, d, z1, y)
    for key in ('W1', 'W2', 'b1', 'b2'):
        network[key]  -= learning_rate * grad[key]

※学習率の値によって学習の効率が大きく異なる → 学習率が大きすぎた場合、最小値にいつまでもたどり着かず発散してしまう → 学習率が小さい場合発散することはないが、小さすぎると収束するまでに時間がかかってしまう

※大域的局所解

勾配降下法のアルゴリズム

• Momentum
• AdaGrad
• Adadelta
• Adam

確率的勾配降下法(SGD)

確率的勾配降下法	勾配降下法
ランダムに抽出したサンプルの誤差	全サンプルの平均誤差

• メリット
  • データが冗長な場合の計算コストの軽減
  • 望まない局所極小解に収束するリスクの軽減
  • オンライン学習が出来る

確認問題

オンライン学習とはなにか？

    オンライン学習とは学習データが入ってくるたびにその都度、新たに入ってきたデータのみを使って学習を行うもの。学習を行う際に1からモデルを作り直すのではなく、そのデータによる学習で今あるモデルのパラメータを随時更新していく

ミニバッチ勾配降下法

ミニバッチ勾配降下法	確率的勾配降下法
ランダムに分割したデータの集合(ミニバッチ)Dtに属するサンプルの平均誤差	ランダムに抽出したサンプルの誤差

確率的勾配降下法のメリットを損なわず、計算機の計算資源を有効利用出来る → CPUを利用したスレッド並列化やGPUを利用したSIMD並列化

確認テスト

ミニバッチ勾配降下法のEtが何を意味するのか図示

誤差勾配の計算

【数値微分】 プログラムで微小な数値を生成し擬似的に微分を計算する一般的な手法 → 各パラメータそれぞれについて計算するために負荷が大きい → 誤差逆伝搬法を利用する

ディープラーニング開発環境

• ローカル
  • CPU
  • GPU
• クラウド
  • AWS
  • GCP

※価格との兼ね合い

Section5 誤差逆伝搬

誤差逆伝搬法

算出された誤差を、出力層側から順に微分し、前の層前の層へと伝播。 最小限の計算で各パラメータでの微分値を解析的に計算する手法

計算結果(=誤差)から微分を逆算することで、不要な再帰的計算を避けて微分を 算出できる

Jupyterで解説

※ functions.d_reluやfunctions.d_sigmoidの切り替えでの収束確認など

確認テスト

2つの空欄に該当するソースコードを探せ

delta2 = functions.d_mean_squared_error(d, y)

grad['W2'] = np.dot(z1.T, delta2)

実践に繋がるアウトプット

終了課題

※ 課題によって利用しているアルゴリズムが適切か？など見たい

    修了課題について確認(5分)
    Q1. 課題の目的とは? どのような工夫ができそうか 
    Q2. 課題を分類タスクで解く場合の意味は何か 
    Q3. irisデータとは何か2行で述べよ

論文解説

早めに結果の図を見てしまって概要を掴むのも手 考察については細かく読まなくても良いかもしれない

実装をうまくやるための参照として使っている。１ツールとしている どうやって自分の課題に使えるかとして昇華すべし

【ラビットチャレンジ】機械学習：その６ サポートベクターマシーン

ラビットチャレンジ 機械学習：その６

サポートベクターマシン

概要

• 2クラス分類のための機械学習手法
• 線形モデルの正負で2値分類

※ 決定境界はいくつも考えられる

SVMの求め方

• 線形判別関数ともっとも近いデータ点との距離をマージンという

• マージンが最大となる線形判別関数を求める

• 主問題の目的関数と制約条件 → 最適化問題をラグランジュ未定乗数法で解くことを考える

サポートベクター

• 分離超平面を構成する学習データの、サポートベクターだけで残りのデータは不要

ソフトマージンSVM

• サンプルを線形分離できないとき
• 誤差を許容し、誤差に対してペナルティを与える
• マージン内に入るデータや誤分類され たデータに対して誤差を表す変数を導入する

非線形分離

• 線形分離できないとき
• 特徴空間に写像し、そ􏰀空間で線形に分離する
• カーネルトリックを利用

カーネルトリック

• カーネル関数
• 高次元ベクトル􏰀内積をスカラー関数で表現
• 特徴空間が高次元でも計算コストを抑えられる

非線形カーネルを用いた分離

• 放射基底関数カーネル( RBFカーネル・ ガウシアンカーネル)を用いる

【ラビットチャレンジ】機械学習：その５ アルゴリズム

ラビットチャレンジ 機械学習：その５

k近傍法

• 分類のための機械学習法
• ある点から近いk個から自身の分類を決定する手法
• k個のクラスラベルの中で最も多いラベルを割り当てる

特徴

• kの個数を変化させると結果も変わる
• kを大きくすると決定境界􏰁滑らかになる

k平均法(k-means)

• 教師なし学習
• クラスタリング手法
• 与えられたデータをk個のクラスタに分類する

※何個に分ければ良いかをどうやって決めるのか？ → ビジネスの専門家が決めるなど… DeepLearningでもビジネスを理解している人といっしょにシステム構築、評価を実施するなどがプラクティスにはなってきている

k平均法(k-means)のアルゴリズム

• 1) 各クラスタ中心􏰀初期値を設定する
• 2) 各データ点に対して、各クラスタ中心と􏰀距離を計算し、 最も距離が近いクラスタを割り当てる
• 3) 各クラスタ􏰀平均ベクトル(中心)を計算する
• 4) 収束するまで2, 3􏰀処理を繰り返す

【ラビットチャレンジ】機械学習：その４ 主成分分析

ラビットチャレンジ 機械学習：その４

主成分分析

概要

• 多変量データの変数の個数を減らす
  • 情報の損失はなるべく小さくする必要がある
• 具体的には？
  • 学習データの分散が最大になるものを探す

係数ベクトル

• 線形変換後の値が変わる
  • どう求めるのが良い？
    • 変換後のぶんさんが最大となる射影軸を探索
    • ノルム制約を入れて解く
  • ラグランジュ関数を最大にする係数を求めることになる
• ラグランジュ関数を最大化する係数を求める
  • 応用数学のタームで実施した固有値・固有ベクトルを求めるものに帰結する

主成分

• 最大固有値に対応する固有ベクトルで線形変換された特徴量を第一主成分と呼ぶ
• k番目の固有値に対応する固有ベクトルで変換された特徴量を第k主成分と呼ぶ
• 寄与率
  • 変換された特徴量のぶんさんは元データの持つ全分散量とも一致
  • 第k主成分の分散の全分散に対する割合を寄与率という

  ※ 例えば100万データを3次元まで主成分に落とした場合、累積寄与率が70％だとすると、3次元圧縮で70％分のデータを保持しているということになる